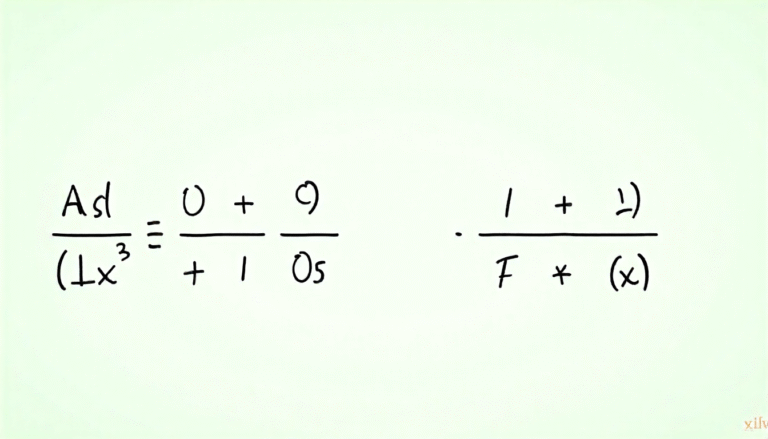Have you ever looked at a set of numbers and wondered what the value between them might be? For example, if you know the temperature at 1 p.m. and 3 p.m., how could you estimate the temperature at 2 p.m.? That’s where an interpolation calculator comes in! It helps you fill in the blanks between known data points quickly and accurately.
In this guide, we’ll explore what interpolation is, how an interpolation calculator works, and why it’s useful in math, science, and even everyday life. Don’t worry — we’ll keep it super simple, fun, and easy to follow.
Table of Contents
What Is Interpolation?

Interpolation is a way to estimate values that lie between two known numbers. Think of it as connecting dots on a graph. If you know two points, you can guess what lies between them by drawing a line or curve through the points.
For example, let’s say you know that a car travels 50 km in 2 hours and 100 km in 4 hours. You can use interpolation to estimate how far it would go in 3 hours.
An interpolation calculator automates this math for you. You just plug in the known points, and it gives you the missing value instantly.
Why Use an Interpolation Calculator?
Math by hand can be slow and tricky. An interpolation calculator saves time and prevents mistakes. It’s like having a smart assistant that understands your data and helps you make sense of it faster.
People use these calculators for many reasons:
- To predict values in data charts
- To estimate measurements in experiments
- To find missing numbers in physics or chemistry tables
- To make smooth graphs and animations in computer graphics
Whether you’re a student, a scientist, or just curious, this tool can make your life easier.
How Does an Interpolation Calculator Work?

At its core, an interpolation calculator uses math formulas to find values between two points. The simplest method is linear interpolation, which assumes the change between two points is straight and steady.
The formula looks like this:
y=y1+(x−x1)×(y2−y1)(x2−x1)y = y_1 + (x – x_1) \times \frac{(y_2 – y_1)}{(x_2 – x_1)}y=y1+(x−x1)×(x2−x1)(y2−y1)
Here:
- x1,y1x_1, y_1x1,y1 = the first known point
- x2,y2x_2, y_2x2,y2 = the second known point
- xxx = the value you want to find yyy for
The calculator applies this formula instantly — no manual math needed.
Types of Interpolation
There are several kinds of interpolation methods, each useful for different data patterns. Let’s look at the most common ones:
1. Linear Interpolation
This is the simplest type. It draws a straight line between two points and assumes the change is steady.
2. Polynomial Interpolation
This uses curves instead of straight lines. It’s useful when data doesn’t follow a straight pattern.
3. Spline Interpolation
This method uses small curves between data points for smoother results. It’s often used in computer graphics and animation.
4. Lagrange Interpolation
This one uses a specific formula for fitting multiple data points at once. It’s a bit advanced but powerful for complex data.
An interpolation calculator may support one or several of these methods depending on its purpose.
Real-Life Examples of Interpolation

Interpolation is not just for math lovers — it’s everywhere!
- Weather Forecasting: Meteorologists use interpolation to estimate temperatures or rainfall between measured locations.
- Finance: Analysts predict stock values or interest rates between recorded times.
- Engineering: Engineers estimate stress, pressure, or speed from known test data.
- Art and Design: In computer graphics, interpolation helps create smooth transitions in animations.
- Science: Researchers fill in missing data in experiments or measurements.
So, the next time you see a smooth graph or a temperature prediction, remember — an interpolation calculator probably helped make it happen!
Step-by-Step: How to Use an Interpolation Calculator
Using an interpolation calculator is super simple. Let’s break it down:
- Gather your known data points.
You need at least two sets of xxx and yyy values. - Enter the known values.
Input the first and second data points into the calculator. - Enter the target xxx value.
This is the point where you want to find the missing yyy value. - Click “Calculate.”
The calculator will instantly show you the estimated yyy value.
That’s it! In seconds, you’ll have your interpolated value without doing the math yourself.
Benefits of Using an Interpolation Calculator
Here are some reasons why people love using these tools:
- Fast and Accurate: No need to worry about calculation errors.
- User-Friendly: Most calculators are easy to use, even for beginners.
- Free and Online: Many are available online at no cost.
- Saves Time: Great for homework, research, or professional work.
- Supports Learning: Helps students understand how interpolation works.
When you use an interpolation calculator, you not only get results — you also see how the math behind it functions.
Interpolation vs. Extrapolation
It’s easy to confuse these two, but they’re different.
- Interpolation finds values within a known range.
- Extrapolation predicts values beyond the known range.
For example, if you know data for 2019 and 2021:
- Finding 2020’s value = interpolation.
- Predicting 2023’s value = extrapolation.
Most interpolation calculators focus on values within the given data range for higher accuracy.
When Not to Use Interpolation
While interpolation is helpful, it’s not perfect. If your data changes suddenly or doesn’t follow a clear trend, interpolation may give wrong results.
For example, if the weather changes drastically between two times, a simple linear interpolation might miss that.
In such cases, use advanced methods like spline interpolation or look for more data points before calculating.
Choosing the Right Interpolation Calculator
There are many calculators online, so how do you pick the best one? Look for:
- Ease of Use: Clear interface and simple inputs.
- Multiple Methods: Support for linear, polynomial, and spline interpolation.
- Graph Display: Some calculators show graphs to visualize results.
- Accuracy: Reliable and precise output.
- Compatibility: Works on desktop and mobile devices.
Some popular tools even let you download results or export data for reports.
Tips for Getting Accurate Results
Here are a few simple tips:
- Use accurate data points. Small mistakes in input can cause big errors.
- Stay within the range of known data.
- If data is uneven or scattered, try a higher-order interpolation method.
- Double-check results using another calculator or manual method.
Remember, the interpolation calculator is only as good as the data you feed it!
Frequently Asked Questions
1. What is an interpolation calculator used for?
It helps estimate unknown values between two known points. It’s used in math, science, engineering, and many other fields.
2. Is an interpolation calculator accurate?
Yes, it’s usually very accurate — especially if your data follows a smooth pattern. The more consistent your data, the better the result.
3. What’s the difference between linear and spline interpolation?
Linear interpolation connects data points with straight lines, while spline interpolation uses curves for smoother transitions.
4. Can I use an interpolation calculator for real-world problems?
Absolutely! It’s used in everything from predicting weather to analyzing business trends.
5. Are interpolation calculators free to use?
Yes, many free online calculators are available. You just enter your data and get results instantly.
6. What’s the formula behind interpolation calculators?
Most use the linear interpolation formula:
y=y1+(x−x1)×(y2−y1)(x2−x1)y = y_1 + (x – x_1) \times \frac{(y_2 – y_1)}{(x_2 – x_1)}y=y1+(x−x1)×(x2−x1)(y2−y1)
It’s simple but powerful for many uses.
Conclusion: Make Math Easier with an Interpolation Calculator
Whether you’re solving a school assignment or working on a professional project, an interpolation calculator can make your life easier. It saves time, improves accuracy, and helps you understand how numbers connect in real life.
The best part? You don’t need to be a math genius to use it. Just enter your data, click “calculate,” and let the tool handle the rest.
So next time you’re stuck between two data points, don’t guess — use an interpolation calculator and find your answer with confidence!