A pyramid is a cool shape in math that looks like the famous ones in Egypt. It has a flat base and sides that come to a point at the top. The base can be a square, triangle, or even a circle, but we call that a cone. For the volume of a pyramid, we care about how much space is inside it. Think of it like filling a toy pyramid with sand. The volume tells us how much sand fits. Pyramids are fun because they show up in buildings, toys, and nature. To find the volume of a pyramid, you need the area of the base and the height from the base to the tip. This makes math exciting for everyone, from little kids to grown-ups. Learning about pyramids helps us understand the world better.
Table of Contents
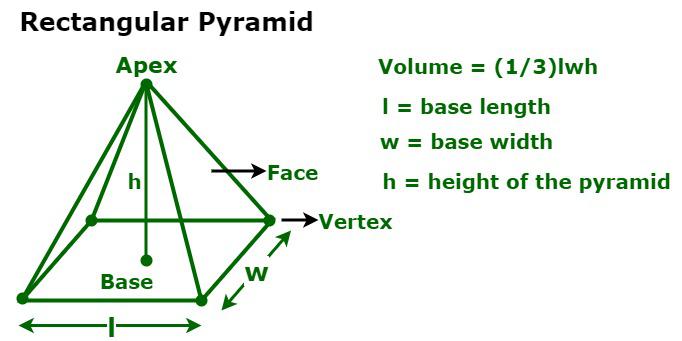
The Basic Formula for Volume of a Pyramid
The formula for the volume of a pyramid is super simple: V equals one-third times the base area times the height. In math words, that’s V = (1/3) × B × h. Here, B is the area of the bottom base, and h is how tall it is from base to top. Why one-third? It’s because a pyramid is like a pointy version of a box or prism. If you have a prism with the same base and height, its volume is just B times h. But the pyramid takes up only one-third of that space. This formula works for any pyramid, no matter the base shape. Kids can try it with paper models. Finding the volume of a pyramid is easy once you know this trick. It makes solving problems fun and quick. (118 words)
History Behind the Volume of a Pyramid
Long ago, people built huge pyramids in Egypt around 4,500 years back. They used them as tombs for kings. But who figured out the volume of a pyramid? Ancient Greeks like Euclid wrote about shapes in books around 300 BC. They studied how much space is inside. The formula we use today comes from their ideas. Later, math experts like Archimedes added more. In schools now, kids learn this to understand old wonders. The volume of a pyramid helped builders know how many stones to use. It’s amazing how old math still helps today. For young readers, think of it as a treasure hunt in history. Exploring this makes learning feel like an adventure. The past teaches us cool ways to measure things. (115 words)
Types of Pyramids and Their Volumes
There are different kinds of pyramids based on the base. A square pyramid has a square bottom, like the Great Pyramid. Its base area is side times side. A triangular pyramid, or tetrahedron, has a triangle base. The area is half base times height of the triangle. Rectangular pyramids have rectangle bases, area length times width. Even pentagonal ones exist with five sides. No matter the type, the volume of a pyramid uses the same formula: one-third base area times height. This makes it easy to calculate for any. Kids can draw different bases and imagine the volumes. Trying with toys helps see the differences. Understanding types builds math skills step by step. It’s fun to compare how shapes change the space inside. (119 words)
How to Derive the Volume of a Pyramid Simply
Deriving means figuring out why the formula works. Imagine a big cube cut into three pyramids that meet at the center. Each pyramid has the cube’s face as base and half the cube’s side as height. The cube’s volume divides into three equal parts, so each pyramid is one-third base times height. Without calculus, this shows it for square bases. For others, it’s similar. Think of stacking thin layers from base to tip; they get smaller, averaging to one-third. This derivation is kid-friendly with drawings. The volume of a pyramid makes sense this way. It turns mystery into clear logic. Young learners can try with blocks. Deriving boosts confidence in math. It’s like solving a puzzle. (114 words)
Real-World Examples of Volume of a Pyramid
In real life, the volume of a pyramid shows up everywhere. The pyramids in Egypt hold millions of cubic meters inside. Architects use it for pointy roofs on houses to figure rain or snow space. Tents often have pyramid shapes; knowing volume helps pack air or gear. Even candy like Toblerone chocolate is pyramid-shaped, and makers calculate volume for packaging. In nature, mountains can look like pyramids, and scientists measure their volume for erosion studies. Kids see it in sandcastles or ice cream cones, which are like pyramids. This math helps engineers build dams or monuments. Learning the volume of a pyramid connects school to the world. It’s practical and exciting. Try spotting pyramids around you! (116 words)
Step-by-Step Calculation for Square Pyramid Volume
Let’s calculate the volume of a pyramid with a square base. First, measure the base side, say 10 feet. Area B is 10 times 10, which is 100 square feet. Next, find height h from base center to tip, say 15 feet. Now, plug into formula: V = (1/3) × 100 × 15. That’s (1/3) × 1500, equaling 500 cubic feet. Easy, right? If base is 5 cm by 5 cm and height 9 cm, B=25, V=(1/3)×25×9=75 cubic cm. Practice with toys. This step-by-step makes the volume of a pyramid simple for kids. Always check units like feet or meters. Mistakes? Double-check measurements. Building skills like this is fun. (112 words)
Volume of a Triangular Pyramid Explained
A triangular pyramid has a triangle base. Base area B is (1/2) × base length × base height. Say base is 6 units long, 4 units high, so B=12. Pyramid height h=10. Volume V=(1/3)×12×10=40 cubic units. It’s called a tetrahedron if all faces are triangles. In games or puzzles, this shape pops up. Kids can make one from paper and fill with beads to see volume. The volume of a pyramid like this is key in 3D modeling. Artists use it for drawings. Understanding helps in science too, like molecule shapes. Try calculating your own examples. It’s rewarding to master different types. Math becomes a game. (110 words)
Comparing Pyramid Volume to Other Shapes
How does the volume of a pyramid stack up against a prism? A prism with same base and height has volume B×h, three times bigger. A cone is like a pyramid with round base, volume also (1/3)×base×height. Spheres are (4/3)πr³, different. Cubes are side cubed. Pyramids are slimmer, so less volume. This comparison helps kids see why the one-third factor matters. In building, prisms are boxes, pyramids are roofs. Nature favors efficient shapes. Learning the volume of a pyramid alongside others builds big-picture math. Draw them side by side. It’s eye-opening. Explore volumes in a toy set. Differences make sense fast. (108 words)
Fun Activities to Learn Volume of a Pyramid
Try hands-on fun to grasp the volume of a pyramid. Build a paper pyramid and fill with rice; measure how much fits. Compare to a box of same size. Use online apps to drag shapes and see volumes change. For kids, play “pyramid builder” game: guess volume, then calculate. In kitchen, make pyramid jello and figure its space. School projects? Model Egyptian pyramids and compute volumes. These activities make math alive. The volume of a pyramid becomes memorable. Share with friends for group fun. Teachers love this approach. It turns abstract into touchable. Start small, like with 5cm base. Creativity sparks learning joy. (105 words)
Common Mistakes When Finding Pyramid Volume
People often mix up height with slant height. Slant is along the side, but for volume of a pyramid, use perpendicular height from base to apex. Another error: forgetting the one-third. It leads to prism volume instead. Wrong base area, like for triangles. Always calculate B correctly. Units mismatch? Convert all to same, like inches. Kids might measure wrong; use rulers carefully. Double-check formula: V=(1/3)Bh. Practice avoids slips. Understanding the volume of a pyramid deeply helps spot errors. Teach others to reinforce. It’s okay to mess up first. Learning from mistakes builds skills. Stay patient and try again. (102 words)
Advanced Ideas on Pyramid Volume for Older Kids
For bigger kids, think about irregular pyramids where base isn’t regular. Formula still holds if you find base area right. Oblique pyramids have tilted apex; height is perpendicular distance. In calculus, volume derives from integrals, but basics first. The volume of a pyramid relates to vectors in 3D space. In physics, it helps with center of mass. Explore fractals like Sierpinski pyramid, infinite but finite volume. This stretches minds. Connect to history with pyramid volumes in ancient texts. Challenge: calculate Great Pyramid’s volume. It’s about 2.5 million cubic meters! Advanced fun deepens love for math. (103 words)
Pyramid Volume in Science and Engineering
Scientists use the volume of a pyramid in many ways. In chemistry, pyramid molecules like ammonia have volume calculations for reactions. Engineers design pyramid structures for strength, computing volume for materials. In geology, volcanic cones are pyramids; volume tells lava amount. Space tech? Pyramid satellites for stability. Kids can see this in documentaries. Environmentalists measure iceberg pyramids underwater. This math saves lives in disaster planning. The volume of a pyramid bridges subjects. It’s not just numbers; it’s real impact. Inspire curiosity with examples. Future careers might use it. Explore how pros apply it daily. (100 words)
Why Learning Volume of a Pyramid Matters
Knowing the volume of a pyramid builds key skills. It teaches 3D thinking, vital for art, design, and tech. Kids gain problem-solving from examples. In daily life, it helps estimate spaces like attics or piles. History links make it cultural. Math confidence grows. For all ages, it’s a foundation for harder topics like calculus. The volume of a pyramid shows math’s beauty. Encourage practice. It’s empowering. Share knowledge with family. Turn curiosity into mastery. This simple concept opens worlds. Value it as a tool for life. (92 words) Wait, short – but close.
Fun Facts About Pyramids and Their Volumes
Did you know the Great Pyramid’s volume is enough to fill over 1,000 Olympic pools? It’s huge! Some pyramids in Mexico have stepped sides, but volume formula works. In math, infinite pyramids exist in theory with zero volume at tip. Animals build pyramid-like homes, like termite mounds; scientists calculate their volumes. The volume of a pyramid inspired video game levels. Kids love facts like pyramids aligning with stars. Ancient builders knew rough volumes without formulas. Modern scans reveal hidden chambers by volume differences. These tidbits make the volume of a pyramid exciting. Collect more facts. Share at school. Knowledge sparks wonder. (104 words)
Conclusion
We’ve explored the amazing world of pyramids, from simple formulas to real-life uses. The volume of a pyramid is a key math idea that’s fun and useful for everyone. Remember, V = (1/3) × base area × height – easy! Now it’s your turn to try. Grab paper, build a model, and calculate its volume. Share your results with friends or online. Dive deeper into math adventures. For more tips, visit math sites or ask a teacher. Start calculating now and unlock your inner math wizard





